Leggere pag 96, 98, 100
Il parallelepipedo
Il parallelepipedo è un prisma avente per basi due parallelogrammi.
Un parallelepipedo si dice retto se ha gli spigoli laterali perpendicolari alle basi, in caso contrario si dice obliquo (Schemi a pag 96).
Il parallelepipedo rettangolo (Il solido su cui concentriamo la nostra attenzione)
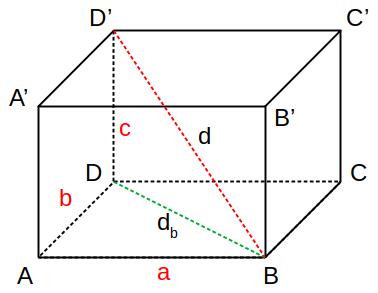
Se le basi di un parallelepipedo sono due rettangoli, esso si dice parallelepipedo rettangolo ed è delimitato da sei rettangoli a due a due congruenti e paralleli.
I tre spigoli che escono da uno stesso vertice di un parallelepipedo rettangolo si dicono dimensioni e sono chiamate:
- lunghezza = a;
- larghezza = b;
- altezza = c.
Le quattro diagonali d di un parallelepipedo rettangolo sono congruenti tra loro.
Area del parallelepipedo rettangolo
Dato che il parallelepipedo rettangolo è un particolare prisma retto, per calcolarne l'area laterale e totale possiamo utilizzare le formule relative al prisma retto
Formule dirette:
Al = 2p * h
At = Al + 2 Ab ricordando che l'altezza h corrisponde allo spigolo c
Formule inverse:
2p = Al / h
h = Al / 2p
Al = At - 2Ab
Ab = (At - Al) : 2
Poiché la base del parallelepipedo rettangolo è un rettangolo
Ab = a * b ovvero prodotto degli spigoli di base
Volume del parallelepipedo rettangolo
Il volume del parallelepipedo rettangolo si ottiene moltiplicando l'area della base per la misura dell'altezza
Formula diretta
V = Ab * h
Formule inverse
Ab = V / h
h = V / Ab
Il volume del parallelepipedo rettangolo si ottiene moltiplicando tra loro le misure delle tre dimensioni lunghezza, larghezza e altezza
Formula diretta
V = a * b * c
Formule inverse
a = V / b * c
b = V / a * c
c = V / a * b
Misura della diagonale del parallelepipedo rettangolo
La misura della diagonale si ottiene estraendo la radice quadrata della somma dei quadrati delle tre dimensioni a, b, c
![]()
Risolviamo insieme il seguente problema
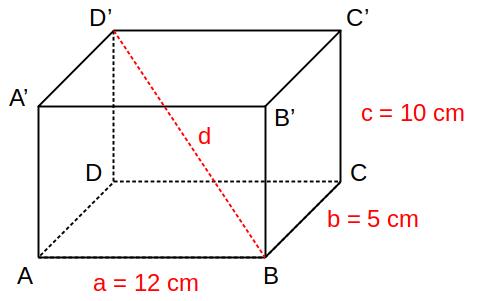
In un parallelepipedo rettangolo, le misure degli spigoli della base sono rispettivamente 12 cm e 5 cm, mentre l'altezza è di 10 cm.
Calcolare:
- la superficie della base;
- l'area laterale;
- l'area totale;
- la lunghezza della diagonale del solido;
- il volume;
- la massa (peso specifico 2,5)
Calcoliamo l'area della base
Ab = a * b = 12 * 5 = 60 cm2
Calcoliamo il perimetro della base (serve per calcolare l'area laterale)
2p = (a + b) * 2 = (12 + 5) * 2 = 34 cm
Calcoliamo l'area laterale
Al = 2p * h = 34 * 10 = 340 cm2
Calcoliamo l'area totale
At = Al + 2Ab = 340 + 2 * 60 = 460 cm2
Calcoliamo la diagonale
d = sqrt(a2 + b2 + c2) = sqrt(122 + 52+ 102) = 16,4 cm sqrt() significa radice quadrata
Calcoliamo il volume con entrambe le formule
V = Ab * h = 60 * 10 = 600 cm3
V = a * b * c = 12 * 5 * 10 = 600 cm3
Calcoliamo la massa (peso)
M = V * ps = 600 * 2.5 = 1500 g ovvero 1,5 kg
Compiti per martedì 10-03-2020:
pag 99 es 5, 6, 7, 8
pag 100 es 2, 3, 6, 8



Comments powered by CComment