Libro di testo a pag 106, 108, 110.
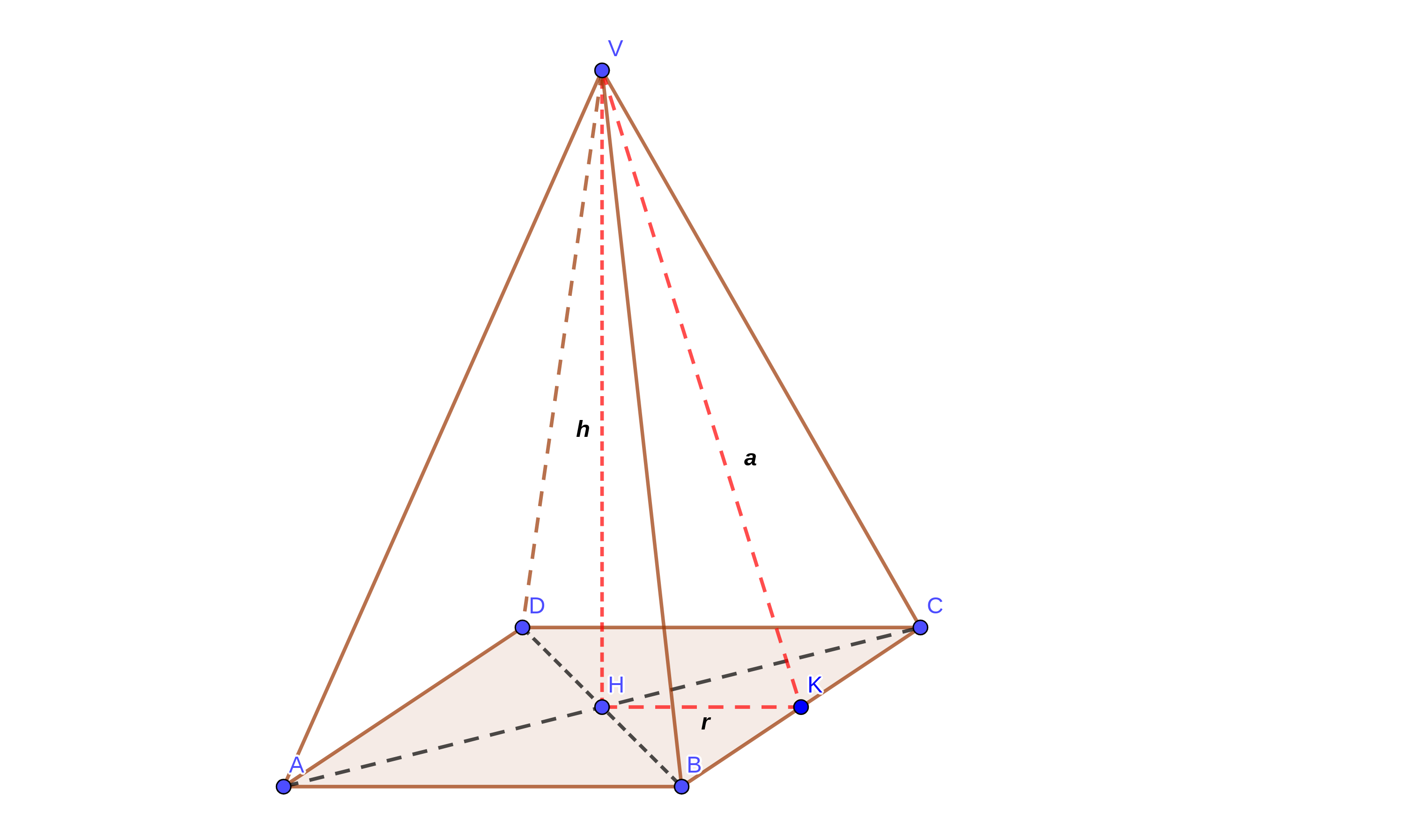
Se la base della piramide è un poligono in cui si può inscrivere una circonferenza e l'altezza della piramide cade nel centro della circonferenza inscritta la piramide si dice retta.
Osserviamo che in una piramide retta le altezze dei triangoli AVB, BVC, CVD, DVA sono congruenti. Ciascuna di queste altezze prende il nome di apotema della piramide.
Formule per il calcolo dell'apotema, del raggio e dell'altezza
Se indichiamo con:
a = apotema
h = altezza
r = raggio della circonferenza inscritta
e applichiamo il Teorema di Pitagora al triangolo VHK otteniamo le seguenti relazioni.
Apotema
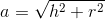
Altezza
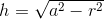
Raggio
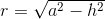
Area laterale e area totale della piramide retta
Consideriamo la seguente immagine che illustra lo sviluppo di una piramide regolare a base quadrata sul piano.
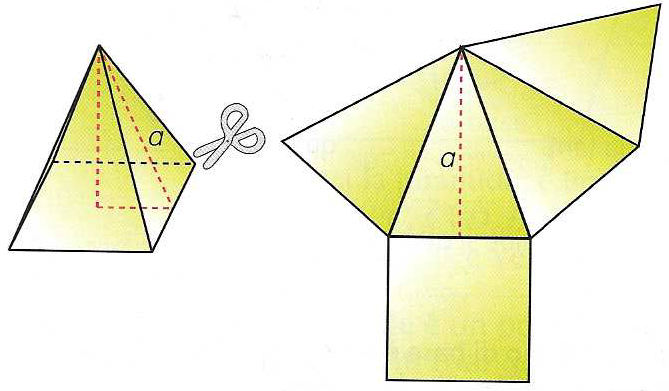
I triangoli che costituiscono le facce laterali della piramide hanno le altezze congruenti e ogni altezza è l'apotema della piramide. per questo, la somma di tutti i triangoli è equivalente a un unico triangolo avente per base il perimetro di base della piramide e per altezza l'apotema della piramide.
L'area laterale della piramide si ottiene moltiplicando il perimetro della base per la misura dell'apotema e dividendo per due il prodotto otenuto.
Area laterale
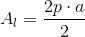
Perimetro
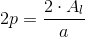
Apotema
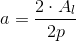
L'area totale At si ottiene addizionando all'area laterale Al l'area del poligono di base Ab
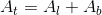
Formule inverse
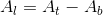
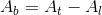
Volume della piramide
Il volume della piramide si ottiene moltiplicando l'area della base per la misura dell'altezza e dividendo il prodotto per 3.
Volume
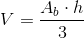
Formule inverse
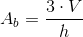
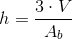
Compiti per martedì 07-04-2020:
cliccare qui per risolvere il problema presente nel modulo di Google inserendo come risultati solo i valori numerici senza unità di misura.



Comments powered by CComment