Libro di testo a pag 298.
Abbiamo già visto che il coefficiente angolare k di una retta determina l'inclinazione della retta stessa rispetto all'asse delle x.
Quindi, se consideriamo due rette r e s con lo stesso coefficiente angolare, significa che sono parallele tra loro.
Rappresentiamo sul piano cartesiano le rette r e s di equazioni:
y = 3x - 1
y = 3x + 2
Costruiamo la tabella dei valori x e y per ciascuna delle due rette.
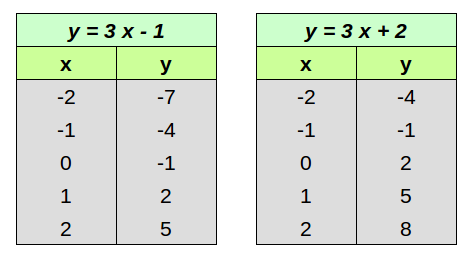
Disegniamo i rispettivi grafici sul piano cartesiano.
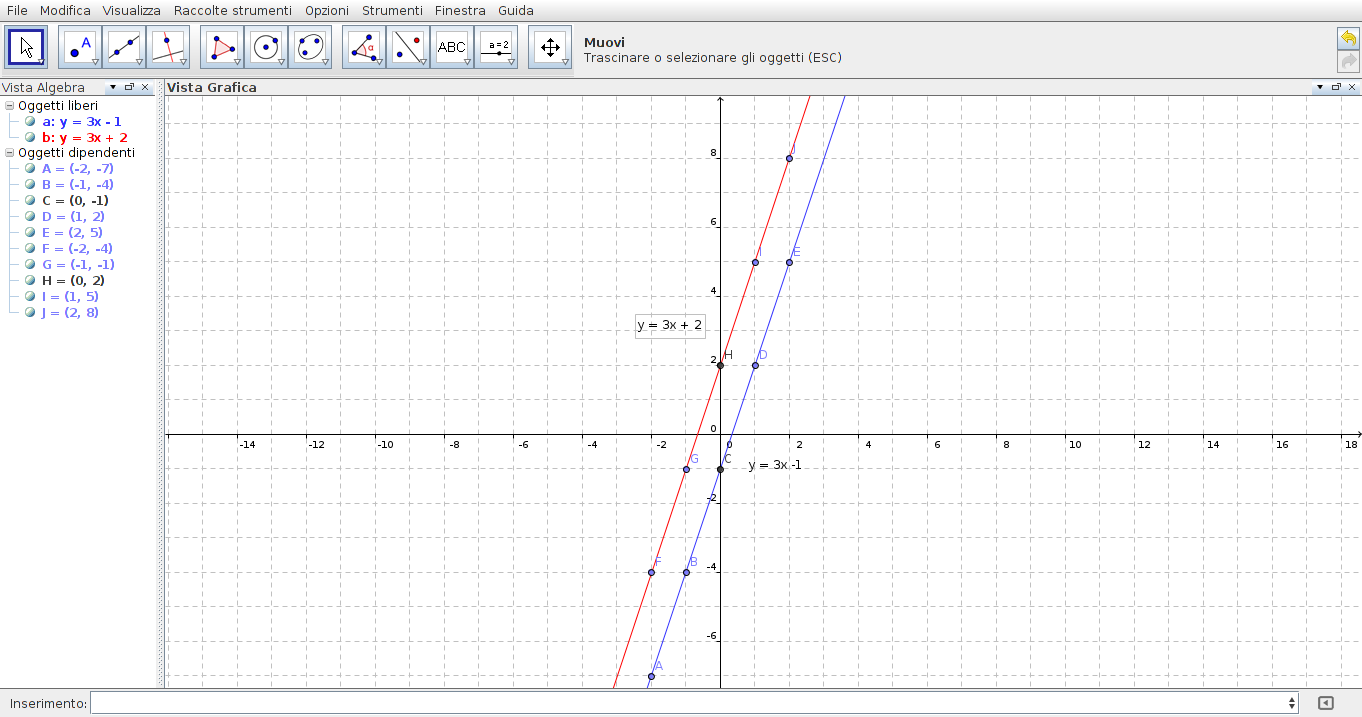
Ci accorgiamo che che le due rette sono parallela tra loro.
In simboli possiamo scrivere r // s
Due rette di equazioni y = kx + q e y = k'x + q' sono parallele se hanno lo stesso coefficiente angolare, cioè se k = k'
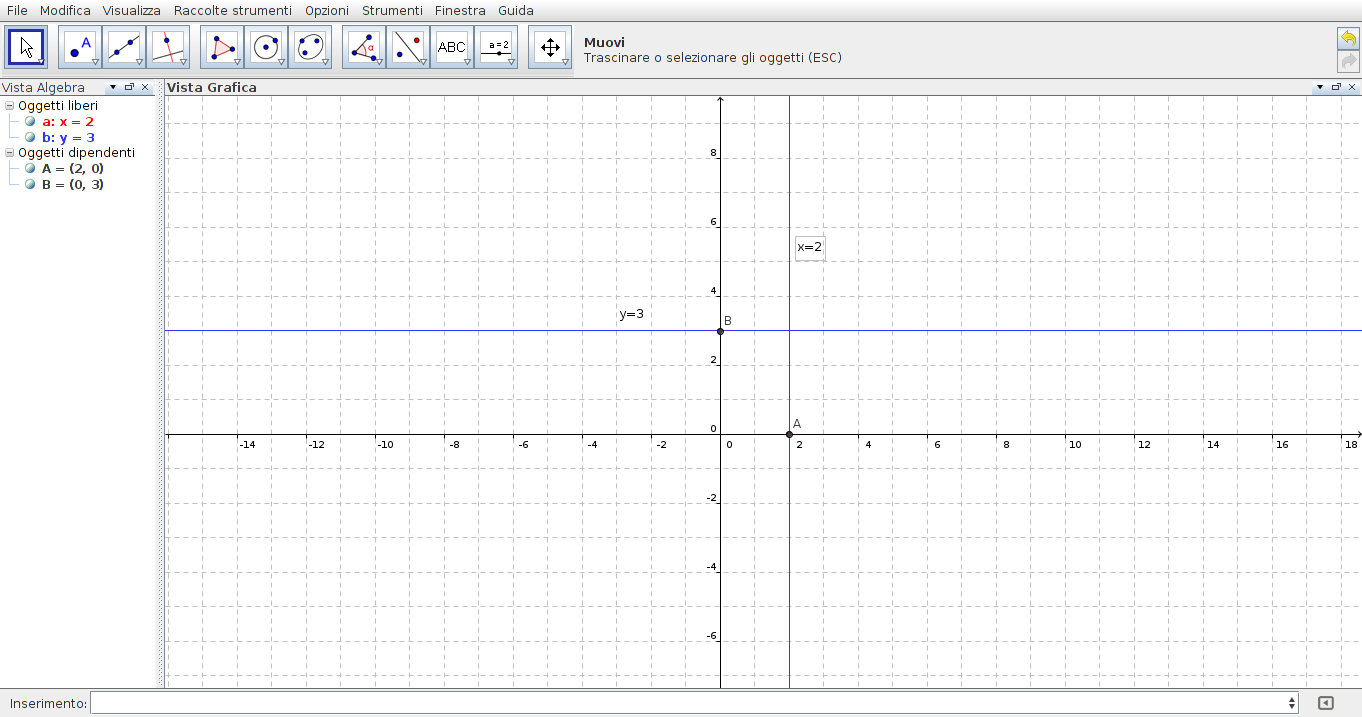
Consideriamo ora la retta di equazione x = 2
Questa retta ha tutti i punti con la stessa ascissa che è 2.
La sua rappresentazione nel piano cartesiano è una retta parallela all'asse delle y.
Consideriamo ora la retta di equazione y = 3
Questa retta ha tutti i punti con la stessa ordinata che è 3.
La sua rappresentazione nel piano cartesiano è una retta parallela all'asse delle x.
L'equazione di una retta parallela all'asse x è del tipo y = k
L'equazione di una retta parallela all'asse y è del tipo x = k
L'equazione dell'asse x è y = 0
L'equazione dell'asse y è x = 0
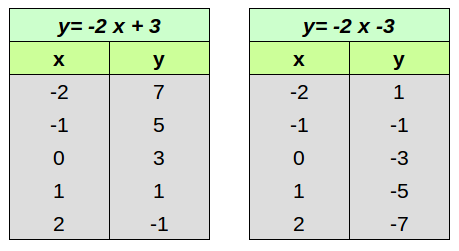
Disegniamo insieme con Geogebra le rette di equazione
y = -2x + 3
y = -2x - 3
Compiti per lunedì 06-04-2020:
Rappresentare le seguenti coppie di rette
y=4x+3
y=4x-5
y=1/2x+4
y=1/2x-2
y=6
y=8
x=5
x=9



Comments powered by CComment