Consideriamo la funzione y = 4x che esprime una funzione di proporzionalità diretta e tracciamo il suo grafico sul piano cartesiano
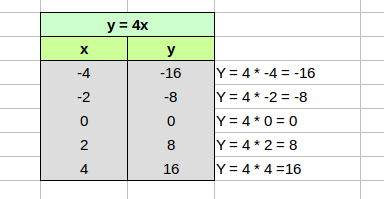
Per farlo costruiamo una tabella inserendo dei valori di x a piacere (x è la variabile indipendente) e ricavando i corrispettivi valori di y sostituendo i valori di x nella funzione.
In questo modo ricaviamo per ciascuna x i corrispondenti valori di y.
Inserendo i punti ottenuti nel piano cartesiano e congiungendoli otteniamo il grafico della funzione y = 4x che è una retta passante per l'origine degli assi.
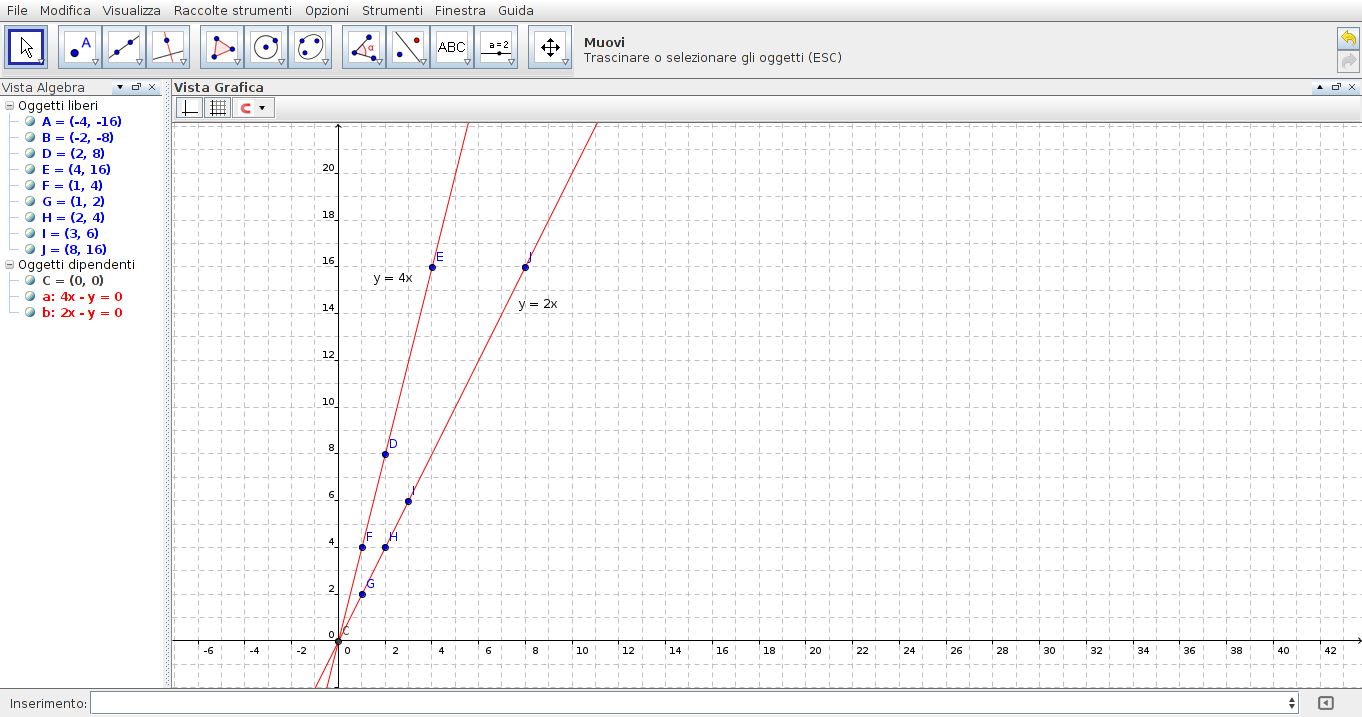
Ora se tracciamo nello stesso grafico la funzione y = 2x possiamo verificare che la sua inclinazione è minore di quella della retta y = 4x. Per questo motivo il coefficiente della x si chiama coefficiente angolare della retta e ne rappresenta l'inclinazione.
Una qualsiasi funzione di proporzionalità diretta è rappresentata dall'equazione y = kx (dove k è un numero reale). Essa ha come grafico una retta passante per l'origine degli assi (0; 0): y = kx si dice equazione della retta per l'origine. Il valore di k determina l'inclinazione della retta rispetto l'asse delle x e si chiama coefficiente angolare della retta.
- se k > 0 la retta si trova nel I e III quadrante;
- se k < 0 la retta si trova nel II e IV quadrante;
- se k = 1 la retta è la bisettrice del I e III quadrante
- se k = -1 la retta è la bisettrice del II e IV quadrante



Comments powered by CComment