La simmetria assiale o ribaltamento, pag 62, 63
Osserva con attenzione il disegno
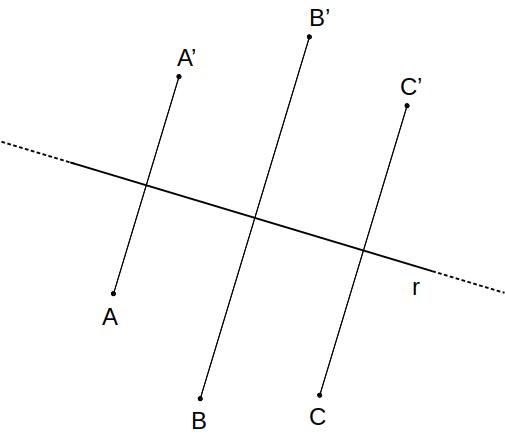
Puoi osservare che:
- le rette contenenti i segmenti AA', BB', CC' sono parallele tra loro;
- queste rette sono tutte perpendicolari alla retta r;
- la distanza del punto A da r è uguale alla distanza del punto A' da r e lo stesso vale per le altre coppie di punti
- la retta r è l'asse dei segmenti AA', BB', CC' (è perpendicolare e passa per i punti medi dei segmenti)
Due punti sono simmetrici rispetto a una retta quando la retta è asse del segmento che unisce i due punti
Nella descrizione di una simmetria assiale si può dire indifferentemente che:
- i punti A e A' sono simmetrici rispetto a r;
- A' è simmetrico di A rispetto a r;
- A è simmetrico di A' rispetto a r;
- A e A' si corrispondono nella simmetria di asse r;
- A' è l'immagine di A nella simmetria di asse r.
Svolgere gli esercizi 1 e 2 a pag 63.
Costruire simmetrie assiali, pag 64, 65
Per trovare il punto P', simmetrico di P rispetto alla retta r
- traccia dal punto P la perpendicolare a r e chiama H il punto di intersezione;
- nel semipiano opposto a quello che contiene P, disegna il punto P' sulla retta HP, tale che PH = HP'
- il punto P' è il simmetrico che cercavi del punto P
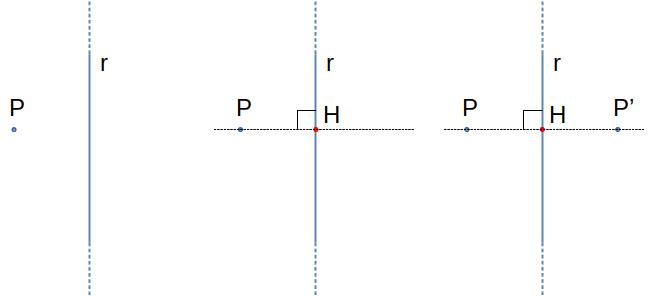
Dato un asse di simmetria r e un punto P, per costruire il simmetrico del punto rispetto all'asse si procede così:
- si traccia la retta perpendicolare all'asse condotta per il punto;
- nel semipiano opposto a quello in cui giace P, si sceglie un punto P' la cui distanza da r sia uguale alla distanza di P da r
Allo stesso modo è possibile costruire il simmetrico di un segmento rispetto a un asse oppure di un poligono.
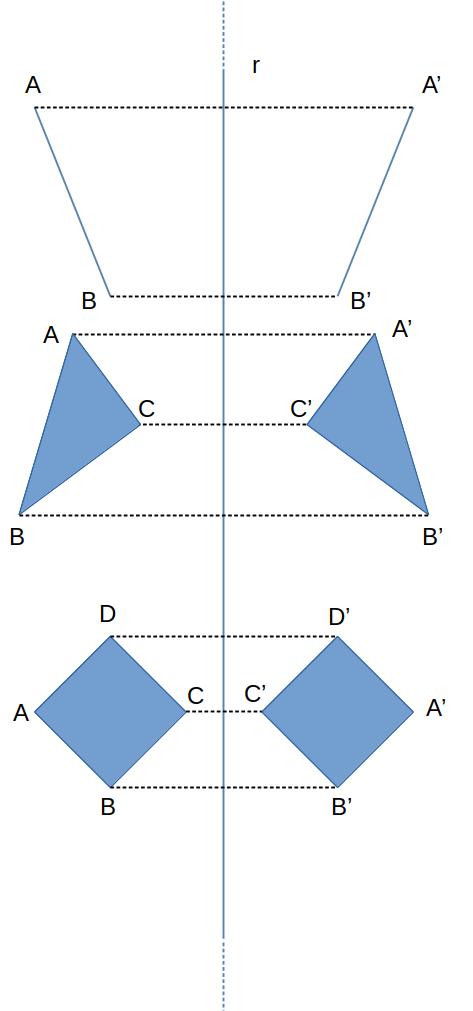
Svolgere gli esercizi 1 e 2 a pag 65.
Compiti per martedì 10-03-2020:
pag 83 es 22
pag 84 es 23, 24, 25, 26
pag 85 es 27, 32
pag 86 es 33, 36
pag 87 es 41
pag 88 es 46, 47, 51



Comments powered by CComment