Per introdurre gli argomenti odierni, leggere da pag 206 a pag 209. Sono pagine descrittive sulle strategie da applicare per svolgere in modo corretto le analisi statistiche.
Gli indicatori statistici che approfondiremo in questa lezione sono 3: moda, mediana e media aritmetica. Possiamo trovarli sul libro di testo da pag 211 a pag 215.
La moda
Analizziamo i voti dell'ultima verifica di matematica riportati dagli alunni di una classe composta da 25 allievi.
Per comodità sono rappresentati in una tabella a due colonne: la colonna di sinistra è il nome dell'alunno, quella a destra indica il voto riportato.
Per comprendere meglio l'andamento della classe è utile costruire una tabella delle frequenze dei voti riportati.
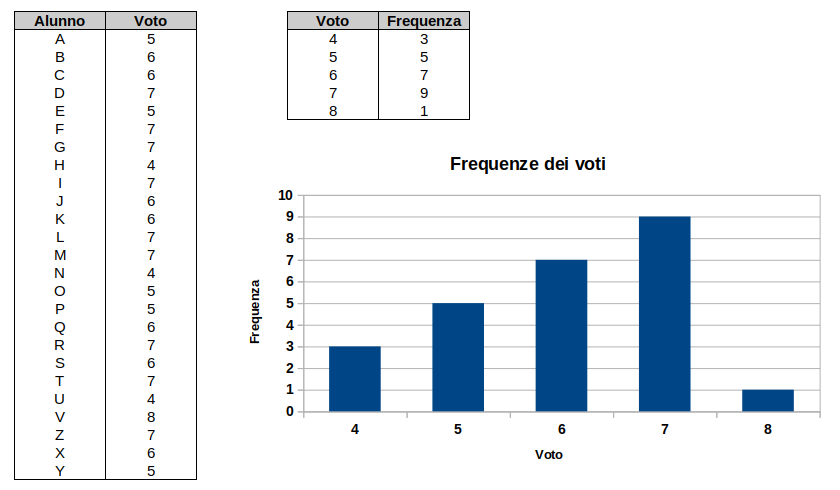
Già dall'osservazione della tabella si intuisce che il voto più frequente è 7, che ha frequenza 9 (9 alunni hanno perso 7 nella verifica).
Per osservare ancora meglio la distribuzione dei voti è utile costruire un istogramma delle frequenze dei voti.
Dall'osservazione del grafico si intuisce facilmente come il voto 7 sia il valore più frequente.
Senza ancora conoscerlo abbiamo ottenuto la moda dei nostri voti.
La moda di un insieme di dati è il valore più frequente.
Nel linguaggio quotidiano siamo abituati a sentire il termine moda: "quelle scarpe sono molto di moda tra i giovani","quel telefono è il modello più di moda quest'anno"....
Dire infatti che qualcosa è "di moda" si riferisce al fatto che è più frequente di altri.
La mediana
Consideriamo ancora i dati dell'esempio precedente e relativi ai voti riportati dagli alunni nell'ultima verifica di matematica.
Rappresentiamo i dati come fatto in precedenza utilizzando una tabella a due colonne. Come fatto prima rappresentiamo a sinistra gli alunni e a destra il voto riportato.
Costruiamo successivamente un'altra tabella ordinando i voti in modo crescente, dal più basso la più alto.
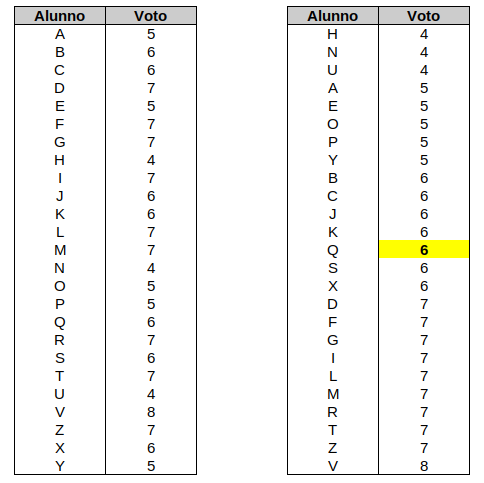
Una volta che i dati sono ordinati in modo crescente, il valore centrale della serie dei dati rappresenta la mediana dei nostri dati (valore evidenziato in giallo).
Nel nostro esempio la mediana è 6 cioè il voto che occupa la posizione centrale nella nostra serie di dati.
La mediana è il numero centrale in un insieme di dati numerici posti in ordine crescente.
Se i dati sono in numero pari (e non dispari come nell'esempio precedente), come valore centrale si prende quello che si ottiene addizionando i due dati centrali e dividendo la loro somma per due.
Esempio: cerchiamo la mediana della seguente serie di numeri:
5 5 6 7 8 10 10 10 11 12
In questo caso i dati sono in numero pari, quindi i numeri candidati sarebbero due, 8 e 10. La mediana si ottiene eseguendo:
(8 + 10) : 2 = 9
La media aritmetica
Consideriamo ancora i dati degli esercizi precedenti. Il professore di matematica vorrebbe conoscere qual è stato l'andamento medio della classe nella verifica.
L'indicatore statistico più adatto per rispondere a questo quesito è il calcolo della media aritmetica.
Si chiama media aritmetica (o semplicemente media) di un insieme di dati numerici la somma dei dati divisa per il numero degli stessi.
Nel nostro esempio si calcola facendo:
(5 + 6 + 6 + 7 + 5 + 7 + 7 +4 +7 +6 +6 +7 +7+ 4 +5 +5 +6 +7+ 6+ 7 +4 +8+ 7 +6 +5) : 25 = 6
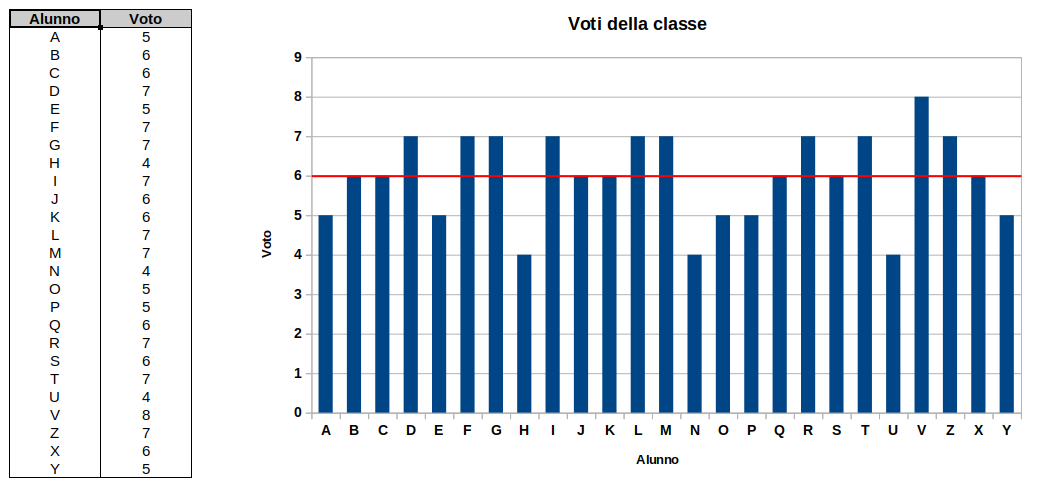
La media dei voti della classe è 6.
Questo risultato può essere anche rappresentato con un istogramma.
Compiti per mercoledì 11-03-2020:
pag 232 es 66, 67, 68, 71, 73
pag 233 es 79, 80
pag 234 es 84, 85



Comments powered by CComment