La lezione è presente sul libro di testo a pag 69, 73, 74, 75.
La simmetria centrale
Fissiamo su un piano due punti distinti O e P e tracciamo la retta r che passa per essi. Poi misuriamo la lunghezza del segmento OP e, sulla stessa retta dalla parte opposta a P, segniamo il punto P' tale che OP = OP'.
I punti P e P' si dicono simmetrici rispetto al punto O.
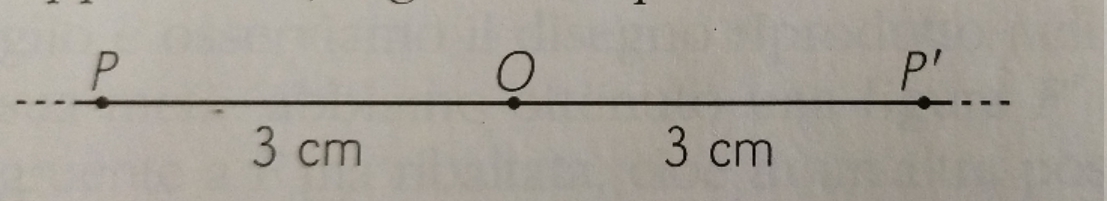
Il punto O si chiama centro di simmetria ed è il punto medio del segmento PP'.
Questa trasformazione geometrica si chiama simmetria centrale di centro O.
La simmetria centrale è una trasformazione geometrica individuata da un punto nel piano, detto centro di simmetria.
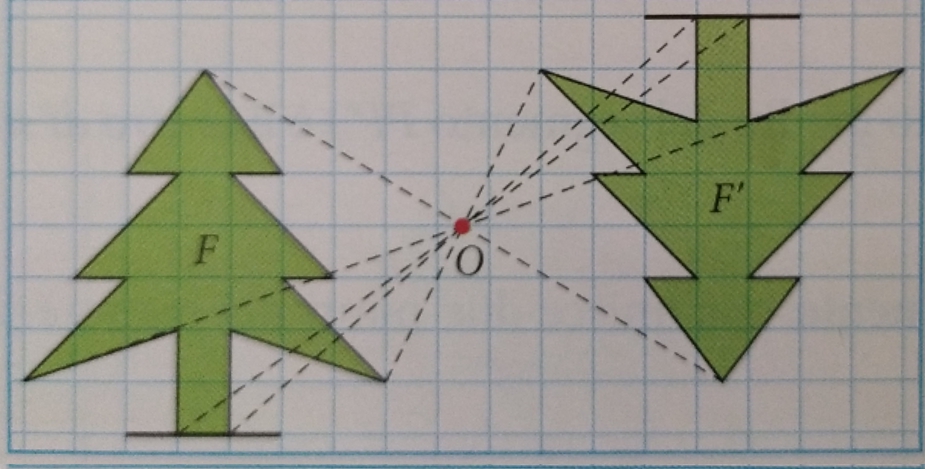
Consideriamo una figura F e costruiamo la sua corrispondente in una simmetria centrale di centro O, nel seguente modo: per ogni punto A, B, C, ... disegniamo il simmetrico rispetto al centro di simmetria O, similmente a quanto abbiamo fatto sopra, e congiungiamo ordinatamente i punti A', B', C', ... così ottenuti.
Se disegniamo in modo accurato possiamo verificare che le due figure che si corrispondono in una simmetria centrale sono congruenti.
Simmetria e poligoni
Simmetria assiale
Osserviamo le seguenti figure:
- il triangolo scaleno non possiede assi di simmetria
- il triangolo isoscele ha un solo asse di simmetria, l'altezza relativa al lato disuguale
- il triangolo isoscele ha tre assi di simmetria, corrispondenti alle altezze relative a ciascun lato
- i deltoidi hanno un solo asse di simmetria
- nei trapezi solo il trapezio isoscele ha un asse di simmetria
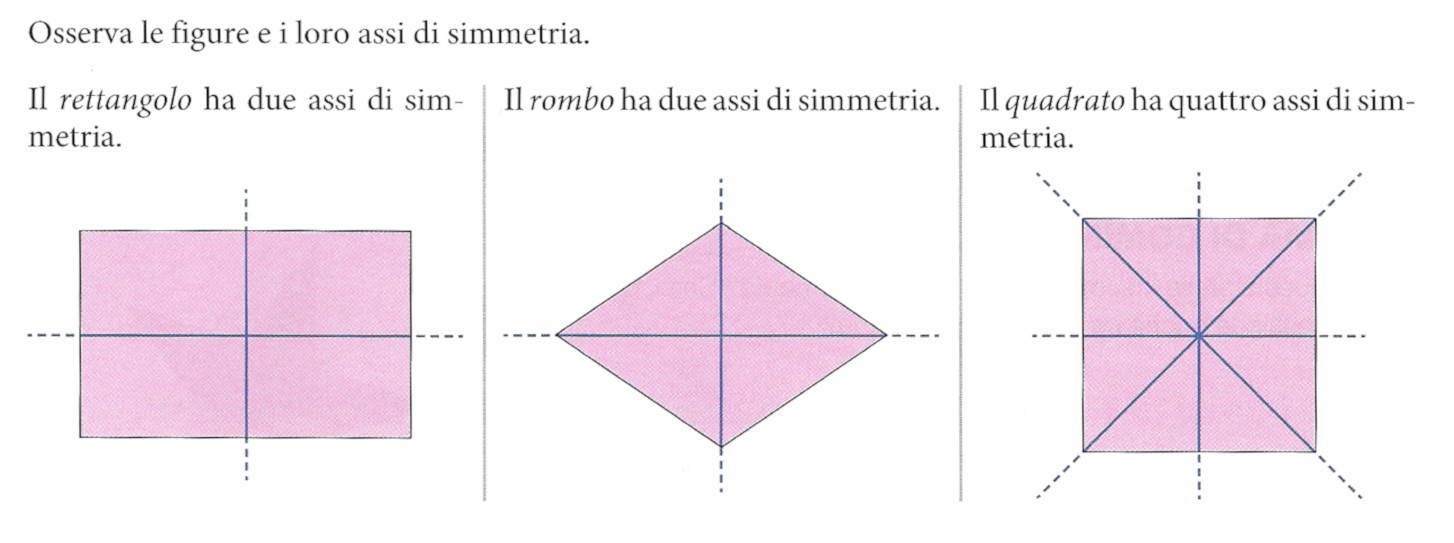
- il rettangolo ha due assi di simmetria
- il rombo ha due assi di simmetria
- il quadrato ha quattro assi di simmetria
Simmetria centrale
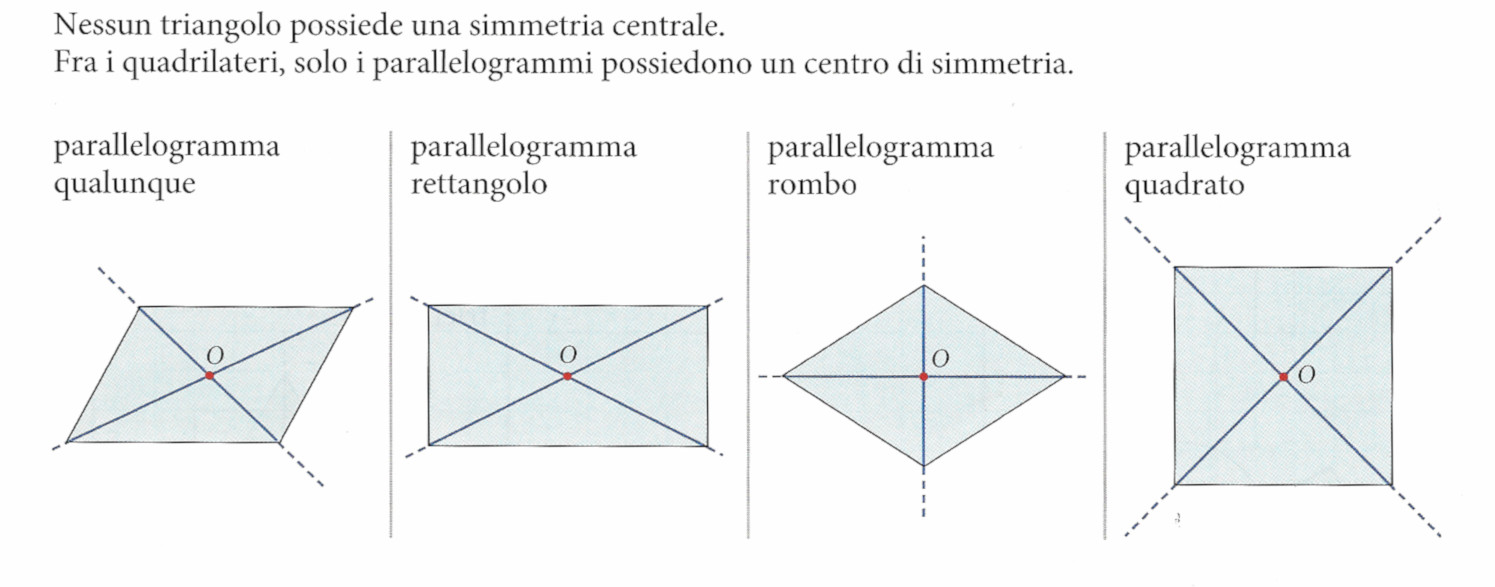
- i triangoli non hanno simmetria centrale
- fra i quadrilateri solo i parallelogrammi possiedono un centro di simmetria
Simmetria e poligoni regolari
Un poligono regolare ha tanti assi di simmetria quanti sono i suoi lati.
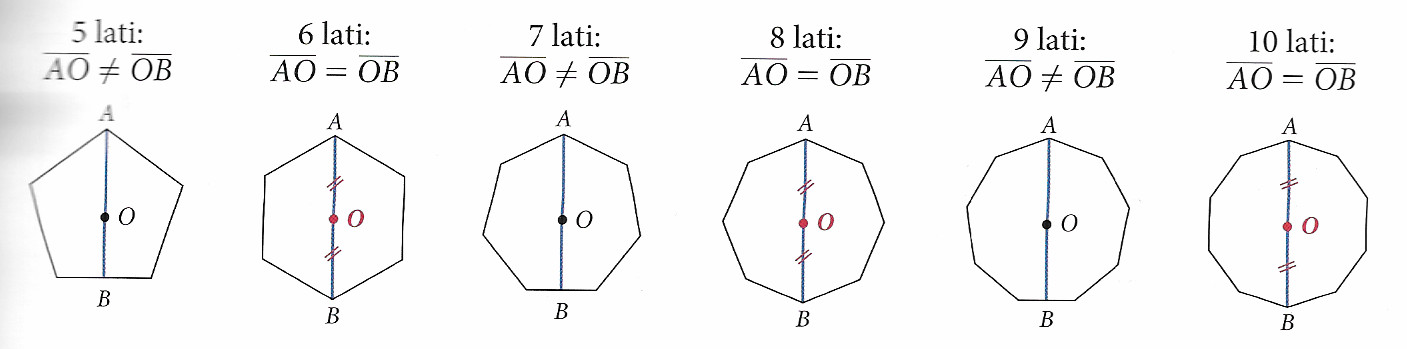
Hanno un centro di simmetria solo i poligoni regolari che hanno un numero pari di lati.
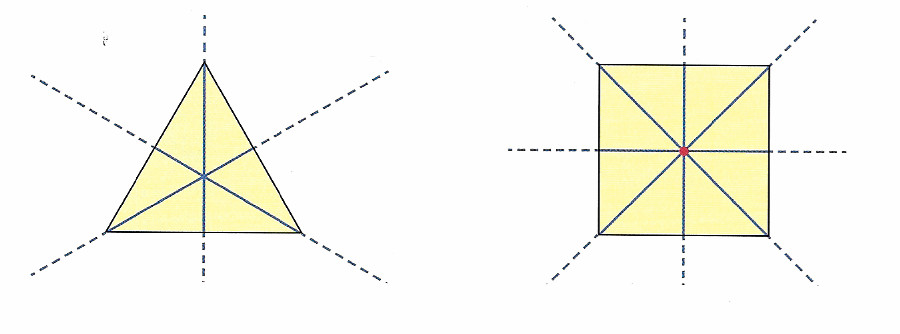
Per esempio il triangolo equilatero ha tre assi di simmetria ma nessun centro di simmetria. Il quadrato possiede 4 assi di simmetria e un centro di simmetria.
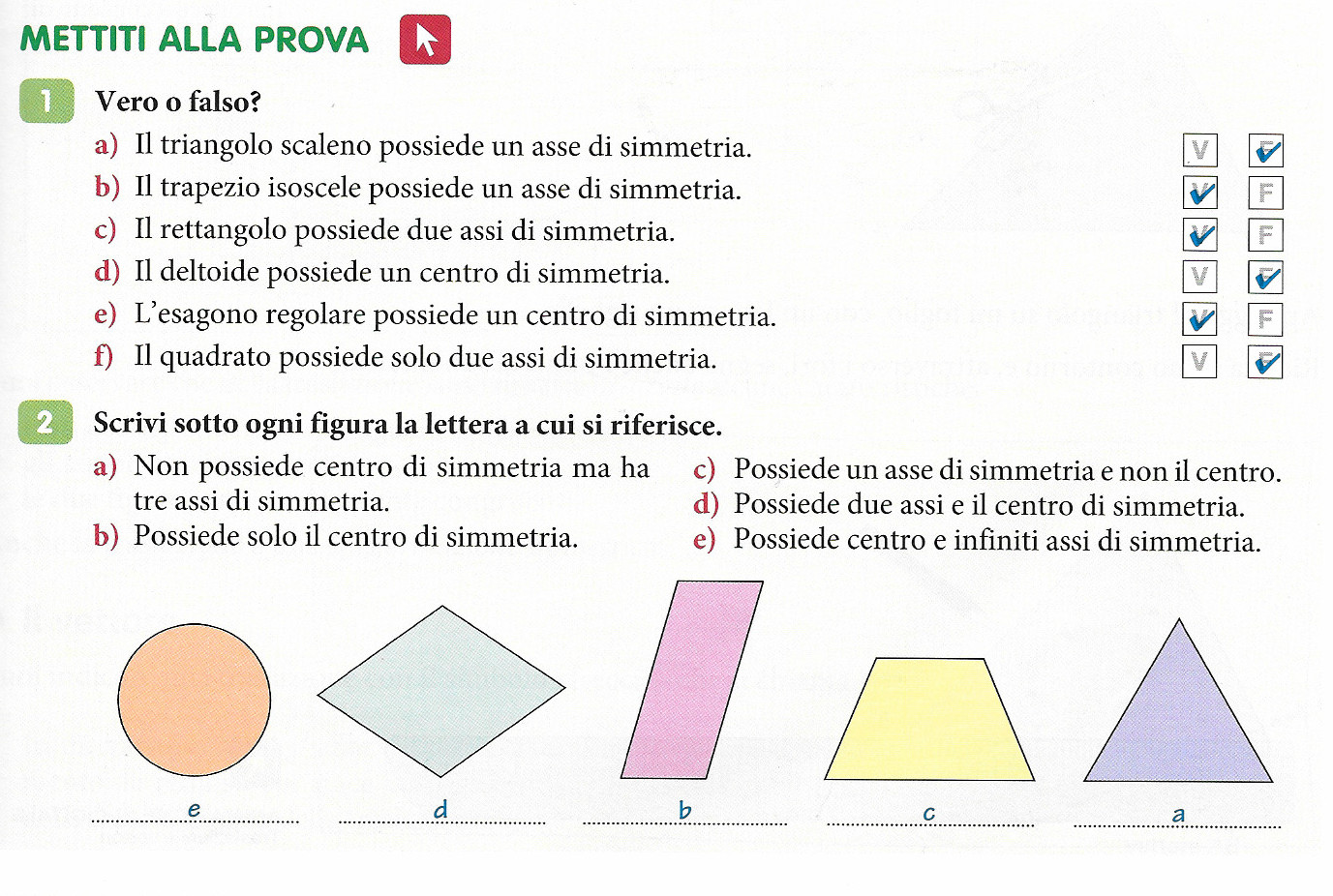
Svolgere gli esercizi 1 e 2 a pag 75
Compiti per martedì 17-03-2020:
pag 99 es dal 120 al 124
pag 100 es 125
Allegate sotto trovate le correzioni
| File | Descrizione | Autore | Dimensione del File |
|---|---|---|---|
 Correzione pag 100 | Davide Zizioli | 722 kB | |
 Correzione pag 99 | Davide Zizioli | 648 kB |
Comments powered by CComment