Libro di testo da pag 216 a pag 219.
Il campo di variazione
Consideriamo i voti di matematica ottenuti da due diverse classi nell'ultima verifica di matematica.
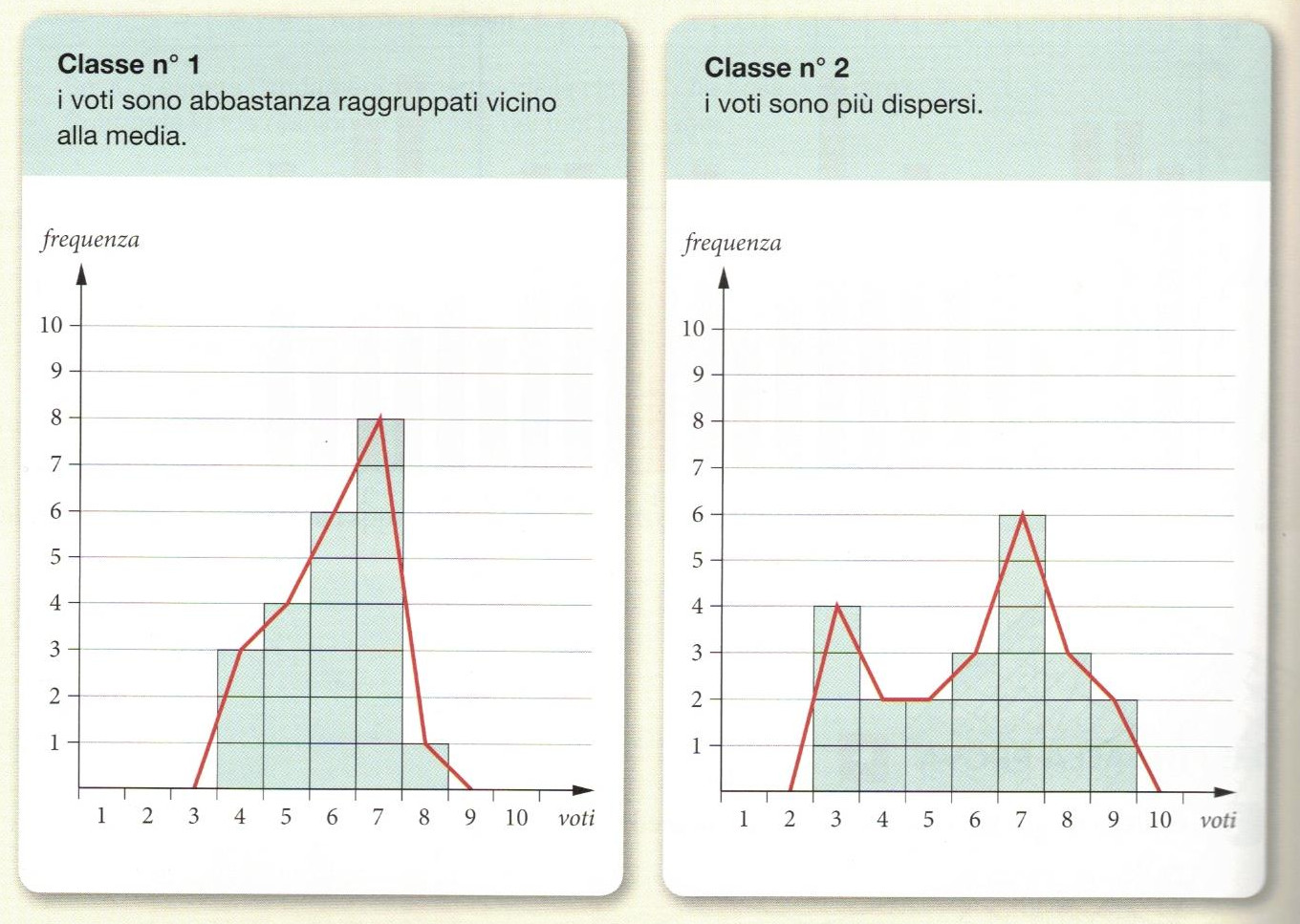
Per entrambe le classi la media aritmetica dei voti ottenuti è 6. Tuttavia possiamo notare che nella classe n° 1 i voti vanno dal 4 all'8 mentre nella classe n° 2 i voti sono più dispersi, infatti vanno dal 3 al 9.
Un esempio di questo tipo è utile per introdurre il concetto di campo di variazione.
Il campo di variazione di un insieme numerico è la differenza fra il valore massimo e il valore minimo.
Il campo di variazione è utile per descrivere la dispersione dei dati, cioè quanto i nostri dati di discostano dalla media aritmetica.
Per le due classi considerate abbiamo la seguente situazione:
- classe n° 1 = 8 - 4 = 4
- classe n° 2 = 9 - 3 = 6
Il campo di variazione della classe n° 2, 6 è maggiore di quello della numero 1.
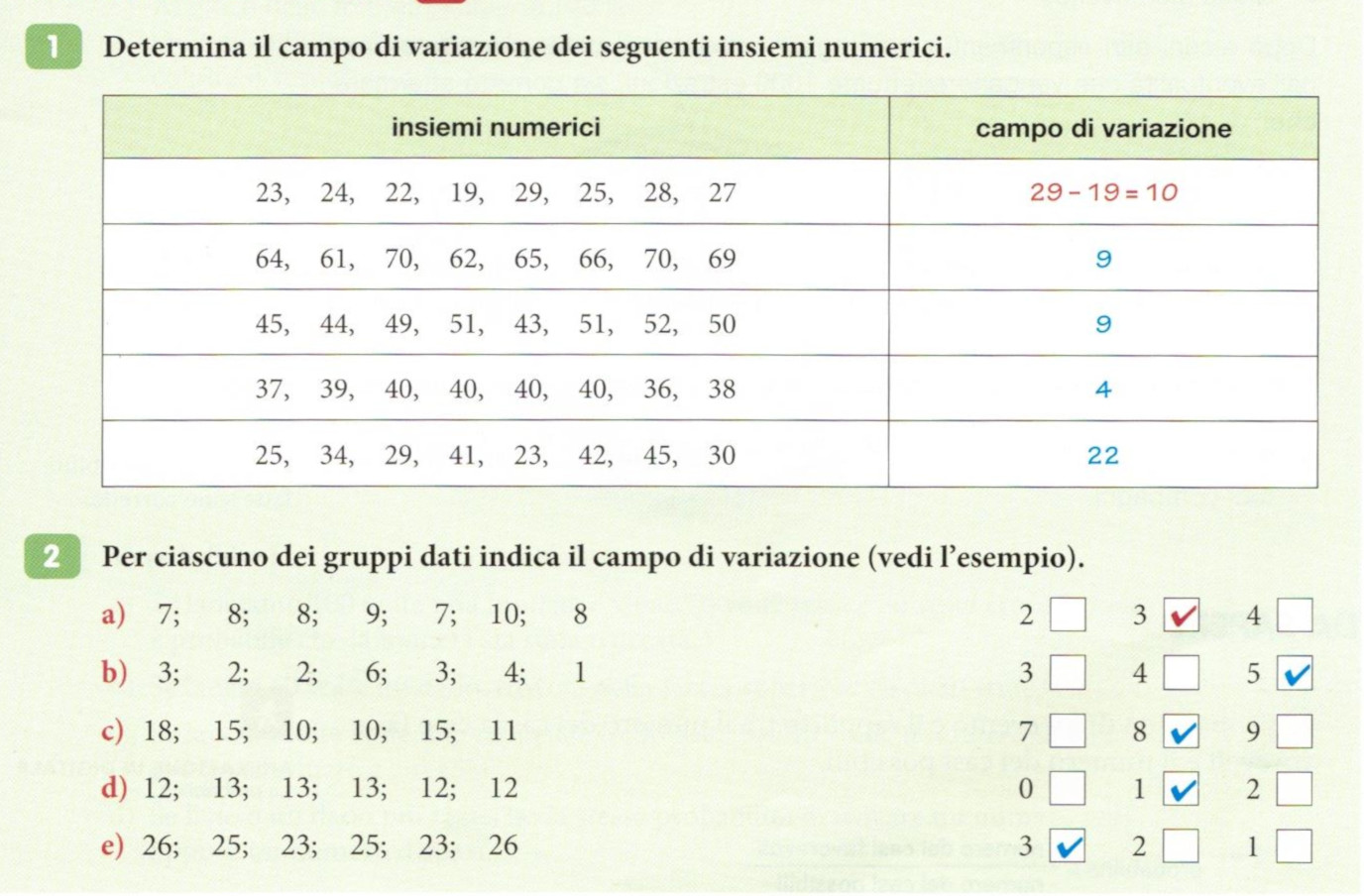
Svolgere gli esercizi 1 e 2 a pag 217.
Previsioni di probabilità
Osservare l'esempio "Prima di cominciare" a pag 218.

Analizziamo insieme il problema.
Gli amici hanno 10 carte suddivise nel seguente modo:
1 A
2 E
3 I
4 O
Le mischiano in un sacchetto (come per estrarre i nomi quando si interroga) e ne estraggono una alla volta per 100 volte, rimettendo sempre la carta estratta dentro al sacchetto.
Dal grafico della frequenza si intuisce che la carta estratta più frequentemente è O (40 volte), mentre la meno frequente è A (9 volte).
Senza ripetere l'estrazione 100 volte si può conoscere la probabilità di un evento, ovvero che esso avvenga, applicando le regole della probabilità:

Lettera A:
casi favorevoli = 1 (la lettera è una sola nel sacchetto)
casi possibili = 10 (le lettere nel sacchetto)
P = 1/10 probabilità di estrarre la lettera A (1/10 si legge 1 su 10)
(1 : 10) * 100 = 10% probabilità in percentuale di estrarre la lettera A
Lettera E:
casi favorevoli = 2 (ho 2 lettere E nel sacchetto)
casi possibili = 10 (le lettere nel sacchetto)
P = 2/10 probabilità di estrarre la lettera E (2/10 si legge 2 su 10)
(2 : 10) * 100 = 20% probabilità in percentuale di estrarre la lettera E
Lettera I:
casi favorevoli = 3 (ho 3 lettere I nel sacchetto)
casi possibili = 10 (le lettere nel sacchetto)
P = 3/10 probabilità di estrarre la lettera I (3/10 si legge 3 su 10)
(3 : 10) * 100 = 30% probabilità in percentuale di estrarre la lettera I
Lettera O:
casi favorevoli = 4 (ho 4 lettere O nel sacchetto)
casi possibili = 10 (le lettere nel sacchetto)
P = 4/10 probabilità di estrarre la lettera O (4/10 si legge 4 su 10)
(4 : 10) * 100 = 40% probabilità in percentuale di estrarre la lettera O
La probabilità di un evento è il rapporto tra il numero dei casi a esso favorevoli e il numero dei casi possibili.
Esercizi di esempio:
In un sacchetto ci sono 3 palline verdi e 7 rosse. Calcola la probabilità di estrarre una pallina rossa.
casi favorevoli = 7 (ho 7 palline rosse nel sacchetto)
casi possibili = 10 (le palline totali nel sacchetto)
P = 7/10 probabilità di estrarre una pallina rossa
(7 : 10) * 100 = 70% probabilità in percentuale di estrarre una pallina rossa
In un sacchetto ci sono 3 palline rosse, 4 gialle e 5 verdi. Calcola la probabilità di estrarre una pallina rossa.
casi favorevoli = 3 (ho 3 palline rosse nel sacchetto)
casi possibili = 12 (le palline totali nel sacchetto)
P = 3/12 è una frazione quindi la semplifico = 1/4 probabilità di estrarre una pallina rossa
(1 : 4) * 100 = 25% probabilità in percentuale di estrarre una pallina rossa
Calcola la probabilità che lanciando un dado esca il numero 3.
casi favorevoli = 1 (esce il numero 3)
casi possibili = 6 (i numeri sulle facce del dado)
P = 1/6 probabilità che esca il numero 3 lanciando il dado
(1 : 6) * 100 = 16,66% probabilità in percentuale che esca il numero 3 lanciando il dado
Calcola la probabilità che lanciando un dado esca un numero pari.
casi favorevoli = 3 (esce il 2, il 4 o il 6)
casi possibili = 6 (i numeri sulle facce del dado)
P = 3/6 è una frazione quindi la semplifico = 1/2 probabilità che esca un numero pari lanciando il dado
(1 : 2) * 100 = 50% probabilità in percentuale che esca un numero pari lanciando il dado
Ovviamente avrò la stessa probabilità (50%) che esca un numero dispari.
Compiti per lunedì 16-03-2020:
pag 236 es 104, 105, 106
pag 237 es 109
pag 238 es 112, 114



Comments powered by CComment