Prof. Davide Zizioli

Svolgiamo insieme l'esercizio numero 108 a pag 195

Uno sgabello è formato da un parallelepipedo rettangolo e da un semicilindro che ne costituisce la seduta. Se le dimensioni si base sono 60 cm e 40 cm e l'altezza è 45 cm, qual è il suo volume? Esprimilo in decimetri cubi.

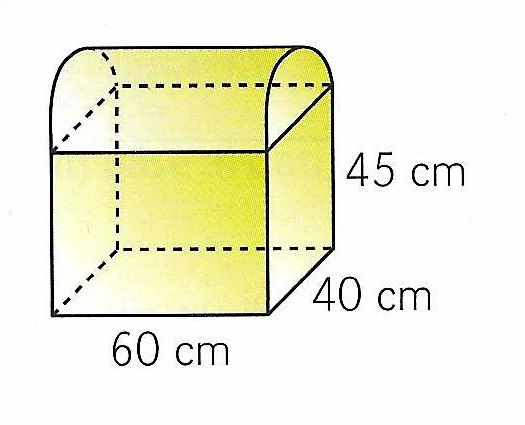
Come potete notare il solido è composto da un parallelepipedo rettangolo sormontato da un semicilindo (metà cilindro).
Le dimensioni della base del parallelepipedo sono 60 cm (a), 40 cm (b) e 45 cm (c).
Consideriamo il semicilindro: la sua altezza corrisponde alla dimensione a del parallelepipedo quindi h = 60 cm; il diametro corrisponde alla dimensione b quindi è 40 cm. Di conseguenza il raggio del cilindro è 20 cm.

DATI
Dimensioni del parallelepipedo
a = 60 cm
b = 40 cm
c = 45 cm
Dimensioni del semicilindro
r = 20 cm
h = 60 cm

Volume del parallelepipedo
V_p = a * b * c = 60 * 40 * 45 cm = 108000 cm³

Area della base del cilindro
A_b = r² *π = 20² * 3,14 = 1256 cm²

Per calcolare il volume del semicilindo posso considerarlo come un cilindro intero e dividere alla fine il volume per 2
Volume del cilindro
V_c = A_b * h = 1256 * 60 = 75360 cm³

Volume del semicilindro
V_s = V_c : 2 = 75360 : 2 = 37680 cm³

Volume del solido (volume del parallelepipedo + volume del semicilindro)
V = V_p + V_s = 108000 + 37680 = 145680 cm³

Trasformiamo in decimetri cubi
145680 cm³ : 1000 = 145,68 dm³

Compiti per giovedì 19-03-2020:
pag 127 es 148