Libro di testo da pag 66 a pag 68.
Le isometrie
Guardiamo insieme le figure del paragrafo "Prima di cominciare".
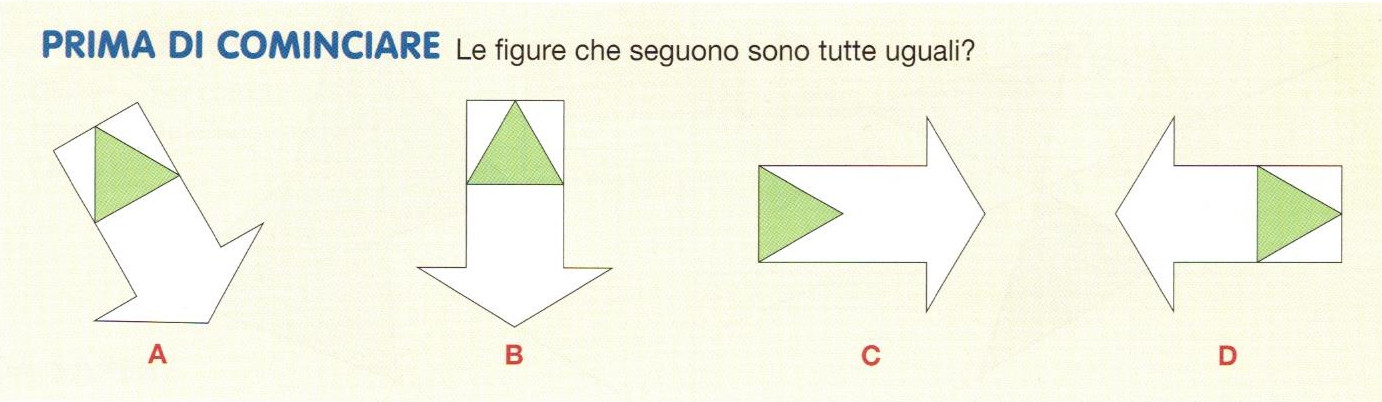
Se focalizziamo la nostra attenzione sui triangoli verdi all'interno delle frecce, possiamo osservare come nel caso C il triangolo verde sia ribaltato. Ne consegue che le figure uguali tra loro sono soltanto A, B e D: esse infatti pur trovandosi in posizioni diverse nello spazio sono perfettamente uguali (congruenti) tra loro.
Osserviamo la figura sottostante: la retta r è l'asse di simmetria dei triangoli 1 e 2. Se confrontiamo le lunghezze dei lati corrispondenti e le ampiezze degli angoli corrispondenti possiamo notare come esse siano perfettamente coincidenti. I triangoli 1 e 2 sono infatti inversamente congruenti.
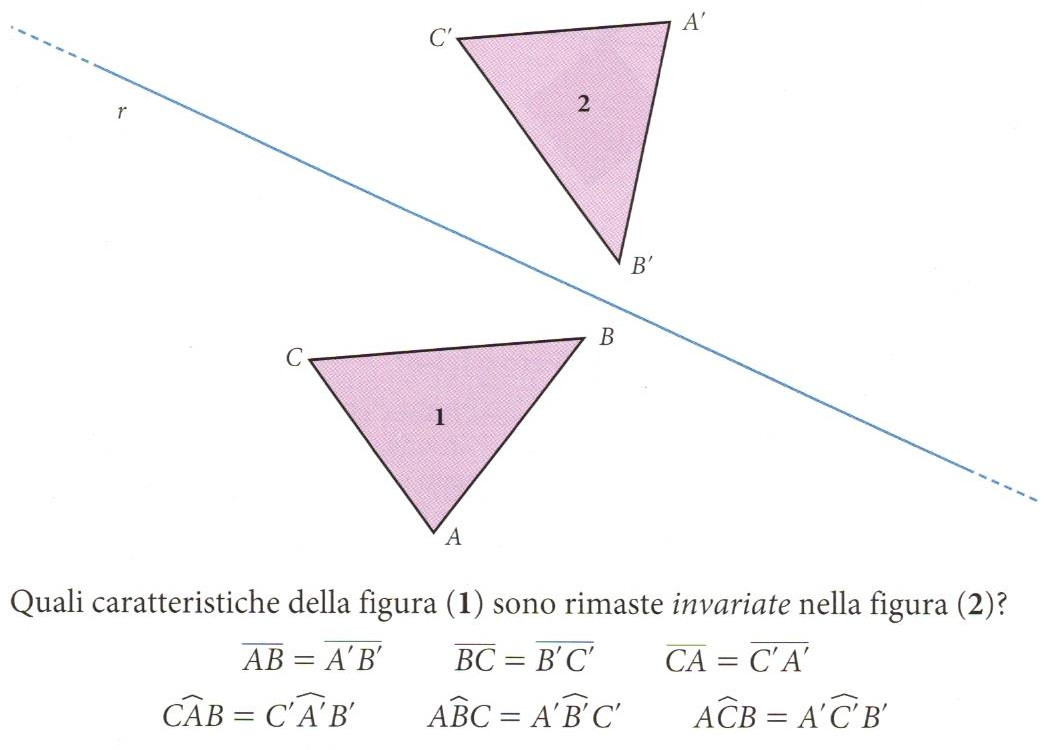
Si dice isometria ogni corrispondenza tra due figure nella quale sono congruenti segmenti corrispondenti e angoli corrispondenti.
Tutte le figure direttamente congruenti (spostamento nel piano) o inversamente congruenti (ribaltamento) sono esempi di figure isometriche.
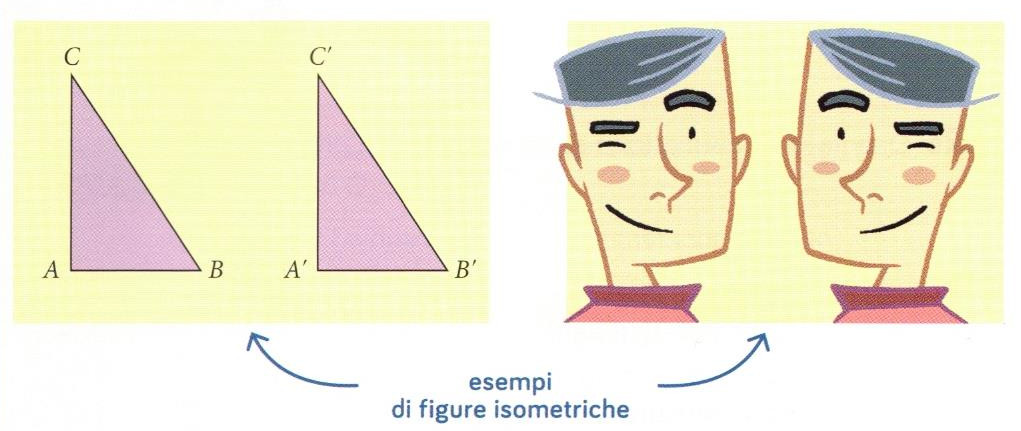
Senza guardare le soluzioni sottostanti, svolgere gli esercizi 1 e 2 a pag 67.

Figure con assi di simmetria
Esaminando alcune figure geometriche, osserviamo che possono essere divise da una retta in due parti simmetriche l'una rispetto all'altra. In questo caso la retta è detta asse di simmetria della figura.
Una figura è dotata di asse di simmetria quando esiste una retta che la divide in due parti simmetriche l'una rispetto all'altra.
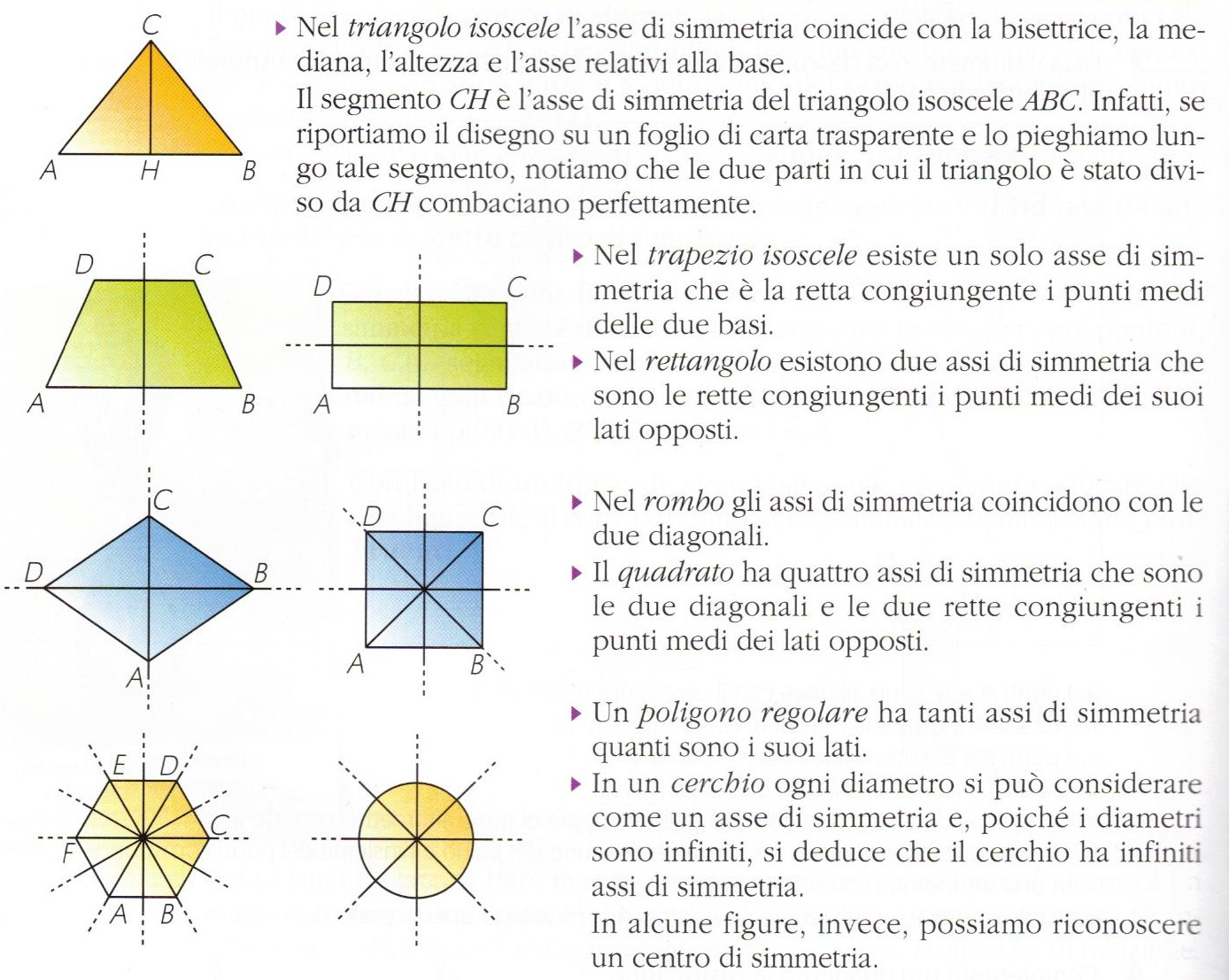
Traccia gli assi di simmetria delle seguenti figure

Confronta i risultati

Compiti per giovedì 12-03-2020:
pag 89 es 57
pag 90 es 59, 60, 61, 62
pag 91 es 64, 66, 67, 68
pag 92 es 72, 73



Comments powered by CComment