Prof. Davide Zizioli

Libro di testo pag 252, 253

Il Massimo Comune Divisore MCD di due o più numeri è il più grande dei divisori che essi hanno in comune.

Esempio: calcoliamo il Massimo Comune Divisore tra i numeri 18 e 30.

Scriviamo l'elenco dei divisore dei due numeri:
D(18)={1, 2, 3, 6, 9, 18}
D(30)={1, 2, 3, 5, 6, 10, 15, 30}
Il più grande dei divisori che hanno in comune i due numeri è il numero 6.
Possiamo quindi scrivere che MCD(18, 30)= 6 

Casi particolari

- 1 è il Massimo Comune Divisore di due o più numeri che hanno l'unità come unico divisore comune. In questo caso i numeri si dicono primi fra loro

MCD(17, 36) = ???
D(17)={1, 17} 
D(36)={1, 2, 3, 4, 6, 9, 12, 18, 36}
MCD(17, 36) = 1

MCD(20, 21) = ???
D(20)={1, 2, 4, 5, 10, 20}
D(21)={1, 3, 7, 21}
MCD(20, 21) = 1

- Dati due numeri, se uno è divisore dell'altro, esso è il Massimo Comune Divisore

MCD(27, 9) = ???
D(27)={1, 3, 9, 27}
D(9)={1, 3, 9}
MCD(27, 9) = 9

MCD(24, 48) = ???
D(24)={1, 2, 3, 4, 6, 8, 12, 24}
D(48)={1, 2, 4, 6, 8, 12, 16, 24, 48}
MCD(24, 48) = 24

Come si calcola il Massimo Comune Divisore di due o più numeri

Possiamo calcolare il MCD in due modi:

1) Si può scrivere l'insieme dei divisori di ciascun numero e selezionare il più grande dei divisori che hanno in comune.

2) Si scompongono i numeri in fattori primi e si calcola il prodotto dei fattori primi comuni, presi una sola volta con l'esponente minore.
Il prodotto ottenuto è il MCD.

Esempi

MCD(72, 48) = ???

1) Scriviamo i divisori dei due numeri e selezioniamo il più grande che hanno in comune
D(72)={1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72}
D(48)={1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
MCD(72, 48) = 24

2) Scomponiamo in fattori primi e consideriamo il prodotto dei fattoti primi comuni presi una sola volta con esponente minore
72 = 2³ x 3²
48 = 2⁴ x 3
MCD(72, 48) = 2³ x 3 = 24

MCD(150, 60) = ???

1) Scriviamo i divisori dei due numeri e selezioniamo il più grande che hanno in comune
D(150)={1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150}
D(60)={1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}
MCD(150, 60) = 30

2) Scomponiamo in fattori primi e consideriamo il prodotto dei fattoti primi comuni presi una sola volta con esponente minore
150 = 2 x 3 x 5²
60 = 2² x 3 x 5
MCD(150, 60) = 2 x 3 x 5 = 30

MCD(210, 140) = ???

1) Scriviamo i divisori dei due numeri e selezioniamo il più grande che hanno in comune
D(210)={1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210}
D(140)={1, 2, 3, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140}
MCD(210, 140) = 70

2) Scomponiamo in fattori primi e consideriamo il prodotto dei fattoti primi comuni presi una sola volta con esponente minore
210 = 2 x 3 x 5 x 7
140 = 2² x 5 x 7
MCD(210, 140) = 2 x 5 x 7 = 70

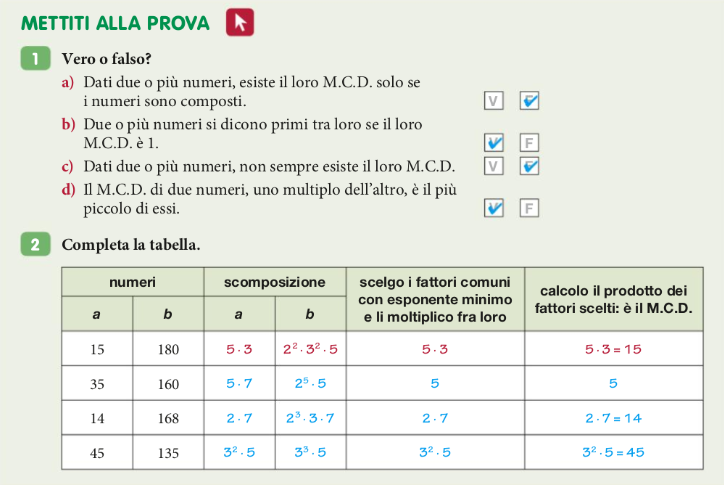
Esercizi 1 e 2 a pag 253

Compiti per giovedì 26-03-2020:
pag 272 es 274
pag 273 es 284, 290, 291 

Allegati:

File	Descrizione	Autore	Dimensione del File
Correzioni pag 272		Davide Zizioli	49 kB
Correzione pag 273		Davide Zizioli	239 kB