Prof. Davide Zizioli

Libro di testo a pag 254, 255

.

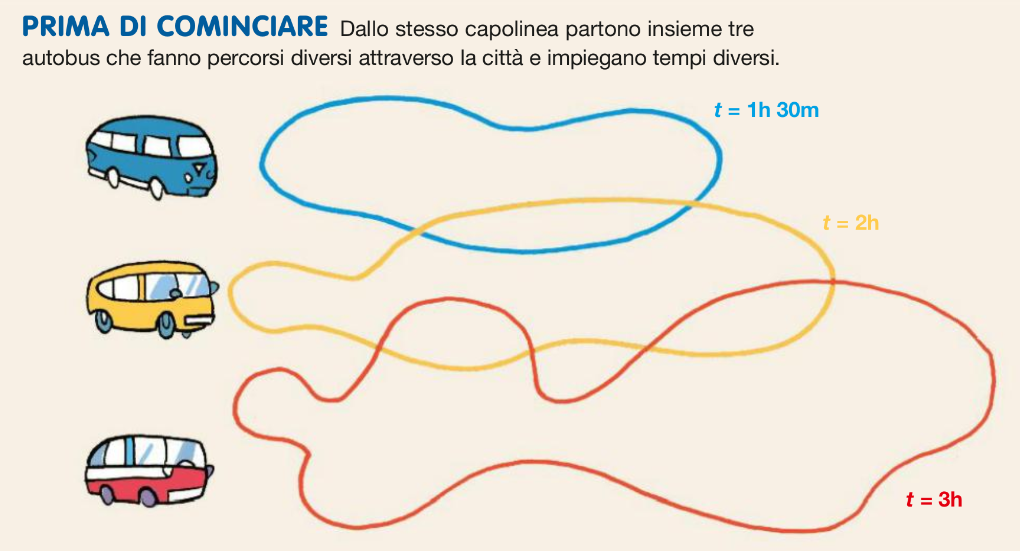Per calcolare dopo quanto tempo i tre autobus si ritroveranno di nuovo insieme al capolinea dobbiamo calcolare il minimo comune multiplo (mcm) tra 1,5; 2 e 3. 

M(1,5)={1,5; 3; 4.5; 6; 7.5; 9; 10,5; 12; ...}
M(2)={2; 4; 6; 8; 10; 12; 14; 16; 18; 20; ...}
M(3)={3; 6; 9; 12; 15; 18; 21; 24; 27; 30 ...}

mcm(1,5; 2; 3) = 6.  I due autobus si ritroveranno insieme al capolinea dopo 6 ore.

Il minimo comune multiplo di due o più numeri è il più piccolo dei loro multipli comuni.

Casi particolari:

- il minimo comune multiplo di due numeri primi tra loro è il loro prodotto
mcm(6; 7)= 42
- dati due o più numeri, se uno di essi è multiplo di tutti gli altri, è anche il loro minimo comune multiplo
mcm(6; 8; 24)= 24
- nella ricerca del mcm di tre o più numeri, si possono trascurare i numeri che sono divisori degli altri numeri
mcm(3; 6; 8)= mcm(6; 8)

Calcolo del mcm mediante la scomposizione in fattori primi.

Per calcolare il minimo comune multiplo di due o più numeri:
- si effettua la scomposizione in fattori primi dei numeri;
- si calcola il prodotto dei fattori primi comuni e non comuni presi una sola volta con esponente maggiore

Esempio:

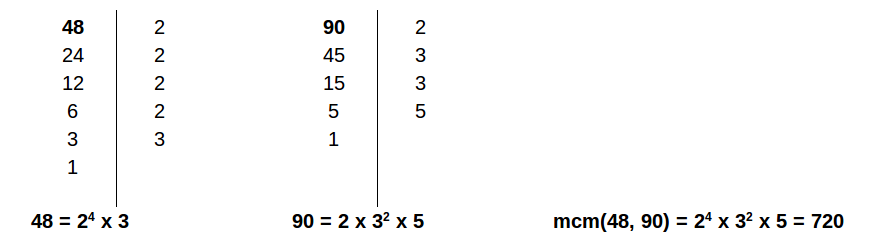
Esempio:

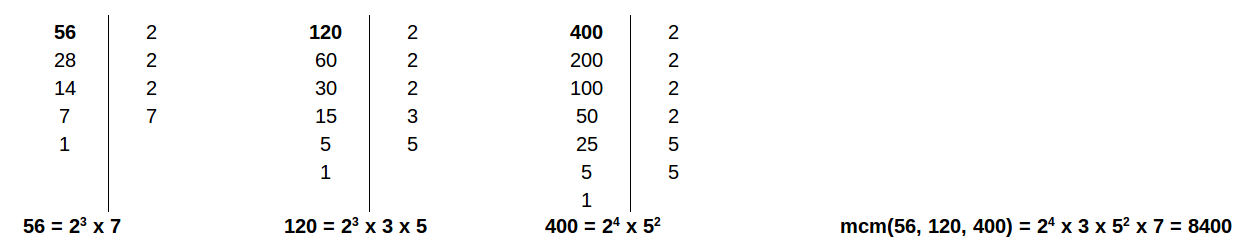
Svolgere gli esercizi 1 e 2 a pag 255

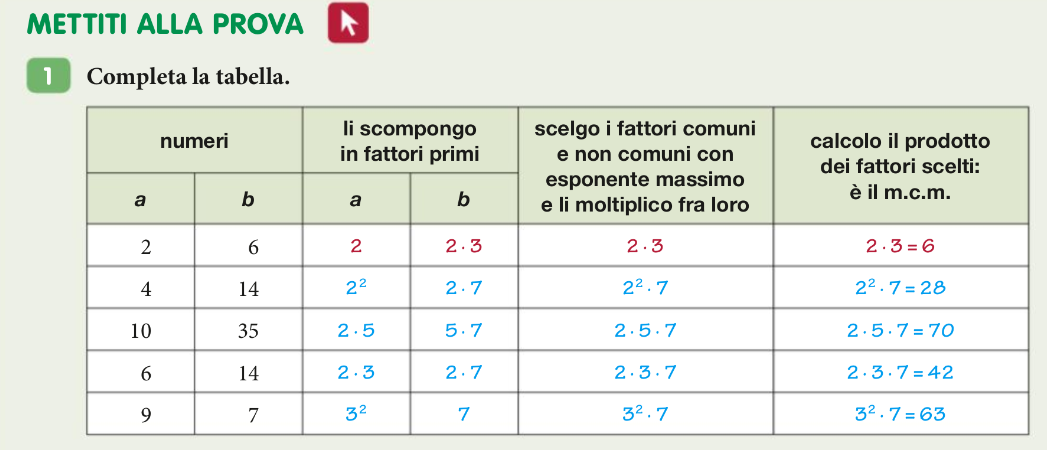
Compiti per mercoledì 08-04-2020:
pag 276 es 335, 336, 337, 338, 339
Le soluzioni sono allegate sotto

Allegati:

File	Descrizione	Autore	Dimensione del File
Correzione pag 276		Davide Zizioli	181 kB